MYP9 Unit 4: Modelling: Linear equations and systems of linear equations
1. Equivalence Transformations
Definition
Equivalence transformations are operations applied to both sides of an equation that do not change the solutions of the equation. These transformations help simplify equations while preserving their equality, making it easier to solve for the variable(s).
Explanation
When solving linear equations, we perform operations such as addition, subtraction, multiplication, or division on both sides of the equation. These operations are known as equivalence transformations. They maintain the equality of the equation and help isolate the variable to find its value.
The main types of equivalence transformations are:
- Addition/Subtraction: Adding or subtracting the same number from both sides of an equation.
- Multiplication/Division: Multiplying or dividing both sides of an equation by the same non-zero number.
Example 1: Solving a Simple Linear Equation
Solve the equation:
\(2x + 3 = 11\)
Solution:
1. Subtract 3 from both sides:
\(2x + 3 – 3 = 11 – 3\)
Simplifying, we get:
\(2x = 8\)
2. Divide both sides by 2:
\(\frac{2x}{2} = \frac{8}{2}\)
Simplifying, we get:
\(x = 4\)
Example 2: Solving a Linear Equation with a Fraction
Solve the equation:
\(\frac{3x}{4} – 5 = 2\)
Solution:
1. Add 5 to both sides:
\(\frac{3x}{4} – 5 + 5 = 2 + 5\)
Simplifying, we get:
\(\frac{3x}{4} = 7\)
2. Multiply both sides by 4:
\(4 \cdot \frac{3x}{4} = 7 \cdot 4\)
Simplifying, we get:
\(3x = 28\)
3. Divide both sides by 3:
\(\frac{3x}{3} = \frac{28}{3}\)
Simplifying, we get:
\(x = \frac{28}{3}\)
2. Solve Systems of Equations with Substitution Method
Definition
The substitution method is a technique for solving systems of equations by isolating one variable in one equation and then substituting that expression into the other equation. This reduces the system to a single equation with one variable, which can be solved using standard algebraic methods.
Explanation
When solving a system of equations using the substitution method, follow these steps:
- Solve one of the equations for one of the variables in terms of the other variable.
- Substitute this expression into the other equation. This will result in a single equation with one variable.
- Solve the resulting equation for the single variable.
- Substitute the solution back into one of the original equations to find the value of the other variable.
- Check the solution by substituting both values into the original equations to ensure they satisfy both equations.
Example 1: Solving a System of Equations
Solve the system of equations:
\(y = 2x + 3\)
\(x + y = 9\)
Solution:
1. Substitute \(y\) from the first equation into the second equation:
\(x + (2x + 3) = 9\)
2. Simplify and solve for \(x\):
\(x + 2x + 3 = 9\)
\(3x + 3 = 9\)
Subtract 3 from both sides:
\(3x = 6\)
Divide both sides by 3:
\(x = 2\)
3. Substitute \(x = 2\) back into the first equation to find \(y\):
\(y = 2(2) + 3\)
\(y = 4 + 3\)
\(y = 7\)
The solution to the system is \(x = 2\) and \(y = 7\).
4. Check the solution by substituting both values into the original equations:
\(y = 2x + 3 \rightarrow 7 = 2(2) + 3 \rightarrow 7 = 7\)
\(x + y = 9 \rightarrow 2 + 7 = 9 \rightarrow 9 = 9\)
The solution is correct.
Example 2: Solving Another System of Equations
Solve the system of equations:
\(3x – y = 4\)
\(2x + y = 1\)
Solution:
1. Solve the second equation for \(y\):
\(y = 1 – 2x\)
2. Substitute \(y\) from the second equation into the first equation:
\(3x – (1 – 2x) = 4\)
3. Simplify and solve for \(x\):
\(3x – 1 + 2x = 4\)
\(5x – 1 = 4\)
Add 1 to both sides:
\(5x = 5\)
Divide both sides by 5:
\(x = 1\)
4. Substitute \(x = 1\) back into the equation \(y = 1 – 2x\) to find \(y\):
\(y = 1 – 2(1)\)
\(y = 1 – 2\)
\(y = -1\)
The solution to the system is \(x = 1\) and \(y = -1\).
5. Check the solution by substituting both values into the original equations:
\(3x – y = 4 \rightarrow 3(1) – (-1) = 4 \rightarrow 3 + 1 = 4\)
\(2x + y = 1 \rightarrow 2(1) + (-1) = 1 \rightarrow 2 – 1 = 1\)
The solution is correct.
3. Solve Systems of Equations with Elimination Method
Definition
The elimination method is a technique for solving systems of equations by adding or subtracting equations in order to eliminate one of the variables. This reduces the system to a single equation with one variable, which can then be solved using standard algebraic methods.
Explanation
When solving a system of equations using the elimination method, follow these steps:
- Align the equations so that like terms are in columns.
- Multiply one or both equations by a constant if necessary to obtain coefficients for one variable that are opposites.
- Add or subtract the equations to eliminate one of the variables.
- Solve the resulting single-variable equation.
- Substitute the solution back into one of the original equations to find the value of the other variable.
- Check the solution by substituting both values into the original equations to ensure they satisfy both equations.
Example 1: Solving a System of Equations
Solve the system of equations:
\(2x + 3y = 13\)
\(4x – 3y = 1\)
Solution:
1. Add the two equations to eliminate \(y\):
\(2x + 3y = 13\)
\(+ 4x – 3y = 1\)
\(6x = 14\)
2. Solve for \(x\):
\( x = \frac{14}{6} = \frac{7}{3} \)
3. Substitute \( x = \frac{7}{3} \) back into one of the original equations to find \( y \). Using the first equation:
\(2\left(\frac{7}{3}\right) + 3y = 13\)
\( \frac{14}{3} + 3y = 13 \)
Multiply everything by 3 to clear the fraction:
\( 14 + 9y = 39 \)
4. Solve for \( y \):
\( 9y = 25 \)
\( y = \frac{25}{9} \)
The solution to the system is \( x = \frac{7}{3} \) and \( y = \frac{25}{9} \).
5. Check the solution by substituting both values into the original equations:
\(2x + 3y = 13 \rightarrow 2\left(\frac{7}{3}\right) + 3\left(\frac{25}{9}\right) = 13 \rightarrow \frac{14}{3} + \frac{75}{9} = 13 \rightarrow \frac{42}{9} + \frac{75}{9} = 13 \rightarrow \frac{117}{9} = 13 \rightarrow 13 = 13\)
\(4x – 3y = 1 \rightarrow 4\left(\frac{7}{3}\right) – 3\left(\frac{25}{9}\right) = 1 \rightarrow \frac{28}{3} – \frac{75}{9} = 1 \rightarrow \frac{84}{9} – \frac{75}{9} = 1 \rightarrow \frac{9}{9} = 1 \rightarrow 1 = 1\)
The solution is correct.
Example 2: Solving Another System of Equations
Solve the system of equations:
\(2x + 3y = 10\)
\(4x + 5y = 22\)
Solution:
1. Multiply the first equation by 2 to set up the elimination of \(x\):
\(2(2x + 3y) = 2(10) \rightarrow 4x + 6y = 20 \)
2. Now subtract the second equation from the new equation to eliminate \(x\):
\(4x + 6y = 20\)
\(- (4x + 5y = 22)\)
\(4x + 6y – 4x – 5y = 20 – 22\)
\(y = -2\)
3. Substitute \(y = -2\) back into the first original equation to find \(x\):
\(2x + 3(-2) = 10\)
Simplifying, we get:
\(2x – 6 = 10\)
Add 6 to both sides:
\(2x = 16\)
Divide both sides by 2:
\(x = 8\)
The solution to the system is \(x = 8\) and \(y = -2\).
4. Check the solution by substituting both values into the original equations:
\(2x + 3y = 10 \rightarrow 2(8) + 3(-2) = 10 \rightarrow 16 – 6 = 10 \rightarrow 10 = 10\)
\(4x + 5y = 22 \rightarrow 4(8) + 5(-2) = 22 \rightarrow 32 – 10 = 22 \rightarrow 22 = 22\)
The solution is correct.
4. Solve Systems of Equations Graphically
Definition
Solving systems of equations graphically involves plotting the equations on a coordinate plane and identifying the point(s) where the graphs intersect. The coordinates of the intersection points represent the solutions to the system.
Explanation
To solve a system of equations graphically, follow these steps:
- Rewrite each equation in slope-intercept form (y = mx + b), if necessary.
- Plot the graph of each equation on the same coordinate plane.
- Identify the point(s) where the graphs intersect. The coordinates of these points are the solutions to the system of equations.
- Check the solution by substituting the coordinates of the intersection point(s) back into the original equations.
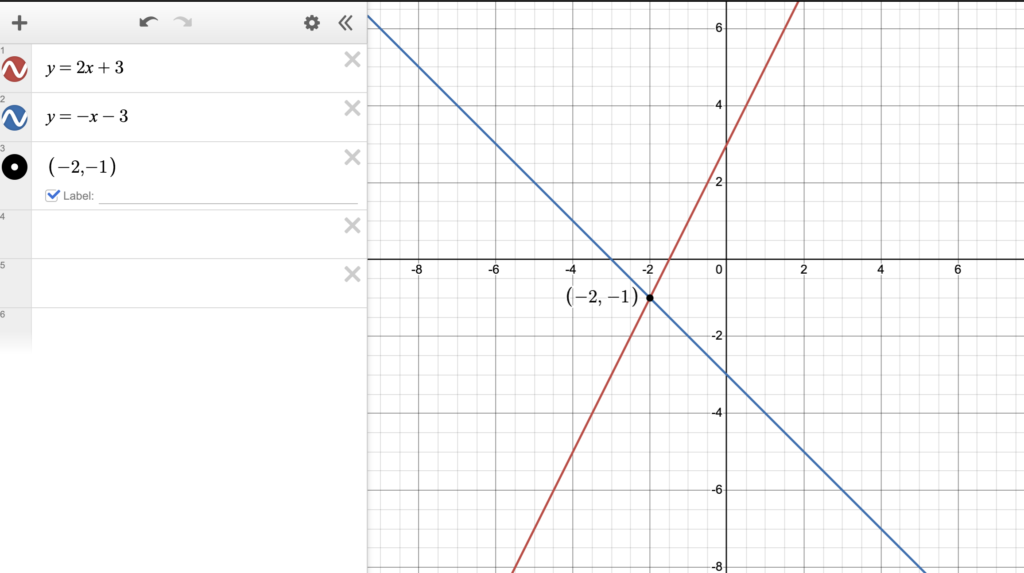
Example 1: Solving a System of Equations Graphically
Solve the system of equations:
y = 2x + 3
y = -x – 3
Solution:
1. Plot the graph of the first equation \(y = 2x + 3\).
2. Plot the graph of the second equation \(y = -x – 3\).
3. Identify the intersection point of the two lines:
The graphs intersect at the point (-2, -1).
4. Check the solution by substituting the coordinates of the intersection point into the original equations:
\(y = 2x + 3 \rightarrow -1 = 2(-2) + 3 \rightarrow -1 = -4 + 3 \rightarrow -1 = -1\)
\(y = -x – 3 \rightarrow -1 = -(-2) – 3 \rightarrow -1 = 2 – 3 \rightarrow -1 = -1\)
The solution (-2, -1) satisfies both equations.
5. Create a Mathematical Model to Solve Real-Life Problems
Definition
A mathematical model is a representation of a real-life situation using mathematical concepts and language. Creating a mathematical model involves translating a problem from the real world into a system of equations, which can then be solved to find solutions that can be interpreted back into the context of the original problem.
Explanation
To create a mathematical model to solve real-life problems, follow these steps:
- Identify the Problem: Understand the real-life situation and identify the variables involved.
- Formulate the Equations: Develop equations that represent the relationships between the variables based on the problem’s conditions.
- Solve the System of Equations: Use appropriate methods (substitution, elimination, graphing) to solve the system of equations.
- Interpret the Solution: Translate the mathematical solution back into the context of the real-life problem and verify its feasibility and accuracy.
Example 1: Fundraising for a School Trip
Problem: A school is organizing a fundraising event to raise money for a school trip. They plan to sell two types of items: T-shirts and mugs. Each T-shirt sells for $20 and each mug sells for $10. The goal is to raise $1000. Additionally, the school wants to sell a total of 70 items. How many T-shirts and mugs should they sell to meet their goal?
Solution:
- Identify the Problem: Let \( x \) be the number of T-shirts sold and \( y \) be the number of mugs sold.
- Formulate the Equations:
- Solve the System of Equations:
- Interpret the Solution: The solution \( x = 30 \) and \( y = 40 \) means the school should sell 30 T-shirts and 40 mugs to meet their fundraising goal of $1000 and sell a total of 70 items.
20x + 10y = 1000
x + y = 70
Solve the second equation for \( y \):
y = 70 – x
Substitute \( y = 70 – x \) into the first equation:
20x + 10(70 – x) = 1000
20x + 700 – 10x = 1000
10x + 700 = 1000
10x = 300
x = 30
Substitute \( x = 30 \) back into the second equation:
y = 70 – 30 = 40
Example 2: Manufacturing Products
Problem: A factory produces two types of products, A and B. Each product A requires 3 hours of labor and 2 hours of machine time, while each product B requires 2 hours of labor and 1 hour of machine time. The factory has 240 hours of labor and 140 hours of machine time available. How many of each product should be produced to maximize the use of resources?
Solution:
- Identify the Problem: Let \( x \) be the number of product A and \( y \) be the number of product B.
- Formulate the Equations:
- Solve the System of Equations:
- Interpret the Solution: The solution \( x = 40 \) and \( y = 60 \) means the factory should produce 40 units of product A and 60 units of product B to maximize the use of resources.
3x + 2y = 240
2x + y = 140
Solve the second equation for \( y \):
y = 140 – 2x
Substitute \( y = 140 – 2x \) into the first equation:
3x + 2(140 – 2x) = 240
3x + 280 – 4x = 240
-x + 280 = 240
-x = -40
x = 40
Substitute \( x = 40 \) back into the second equation:
y = 140 – 2(40) = 140 – 80 = 60
